Problem Statement

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Examples

Example 1

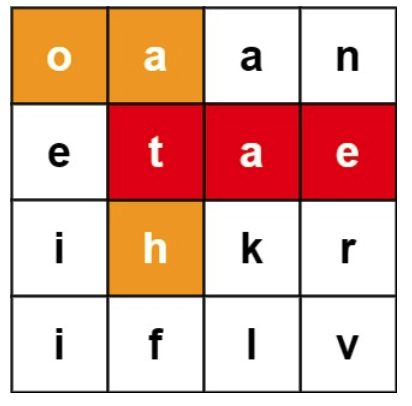
character board

Input:

board = [[“o”,”a”,”a”,”n”],[“e”,”t”,”a”,”e”],[“i”,”h”,”k”,”r”],[“i”,”f”,”l”,”v”]],

words = [“oath”,”pea”,”eat”,”rain”]

Output: [“eat”,”oath”]

Example 2

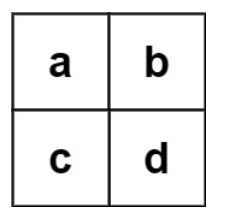
character board

Input:

board = [[“a”,”b”],[“c”,”d”]],

words = [“abcb”]

Output: []

Constraints

m == board.length

n == board[i].length

1 <= m, n <= 12

board[i][j] is a lowercase English letter.

1 <= words.length <= 3 * 104

1 <= words[i].length <= 10

words[i] consists of lowercase English letters.

All the strings of words are unique.

Solution

class TrieNode:
    """
        prefix tree for words
    """
    def __init__(self):
        self.children = {}
        self.isWord = False
    
    def addWord(self, word):
        curr = self # root of the Tree

        for char in word:
            if char not in curr.children: # if current character not in children dictionary keys
                curr.children[char] = TrieNode() # add a trie node

            curr = curr.children[char] # grab the key
        
        # after adding all character, make the leaf node as end of a complete word
        curr.isWord = True

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        # initialize the problem space
        ROWS = len(board)
        COLS = len(board[0])

        # additional memory to keep track of visited word
        result = set()
        visited = set()
        # root of the prefix tree which will have all the words
        root = TrieNode()

        # build the prefix tree
        for word in words:
            root.addWord(word)

        def dfs(r, c, node, word):
            # base case
            if (r < 0 or c < 0 or r == ROWS or c == COLS) \
                or (r, c) in visited \
                or board[r][c] not in node.children:
                return
            
            visited.add((r, c))

            word += board[r][c]
            node = node.children[board[r][c]] # get the key

            if node.isWord: # if we find a full word, add it to result
                result.add(word)
            
            # otherwise traverse
            dfs(r + 1, c, node, word)
            dfs(r - 1, c, node, word)
            dfs(r, c + 1, node, word)
            dfs(r, c - 1, node, word)

            visited.remove((r, c)) # remove from visited to allow backtracking
        

        # traverse each item from the character board
        for r in range(ROWS):
            for c in range(COLS):
                dfs(r, c, root, "")
        
        return list(result)

Complexity Analysis

Time Comlexity

Brute Force Approach

For each word, traverse the board and return true if that word exist in the board

Time for each DFS: Traverse in four direction for each Depth First Search (dfs). In worst case, we need to traverse until the length of the word. So, one dfs will have 4*3^(L-1) where L is the length of a word
Time to Search one Word in the Board: In worst case, the first character of the word we are searching can be situated on board[m - 1][n - 1] index. So, for worst case we need to go (complexity to find the first character in the board) * _(complexity for one word search) = m * n * 4 * 3^(L-1)
Operation #2 happens for each word search. So, total complexity is (number of word search) * (complexity for one word search) = O(W * m * n * 4 * 3^(L-1))

Prefix Trie Approach

Prefix Trie removes the need to search the complete board for each word again and again, instead we will build a prefix tree one time and search the board one time only and grab all the word which exist in the board

Time to Add input words in Trie Data Structure: For each word it will take O(logL), where L is the longest word length. So, for all input words, O(W * logL)
Time for each DFS: Traverse in four direction for each Depth First Search (dfs). In worst case, we need to traverse until the length of the word. So, one dfs will have 4 * 3^(L-1) where L is the length of a word
Traverse the complete board: For worst case we need to traverse the full board if input has words which first characters are a complete set of board’s character. So, for worst case we need to go (complexity to traverse the full board) * (complexity for one word search) = m * n * 4 * 3^(L-1)
So, Overall complexity is
= (complexity to add word in trie) + (complexity to traverse the full board) * (complexity for one word search)
= O(W * logL) + O(m * n * 4 * 3^(L-1))
= O(m * n * 4 * 3^(L-1))

This is a huge improvement if we have large input of words need to search

Space Complexity

Brute Force Approach

Overall space complexity is

= (visited set) + (dfs call stack)

= O(n) + O(logL)

= O(n)